Dérivation ../../logo

Introduction

Nombre dérivé :
Soit une fonction $f$ est dérivable en $a$ si, et seulement, si, la limite existe et est finie :
$$f'(a)=\lim_{h\to\ 0}\frac{f(a+h)-f(a)}{h}.$$ $$f'(a)=\lim_{x\to\ a}\frac{f(x)-f(a)}{x-a}.$$
Présentation de la dérivabilité
On dit que f'(a) est la le nombre dérivé de f en $a$
$a$ étant un point quelconque $\in\ \mathbb{R}$
Activite : 17
Soit $f$ définie sur $\mathbb{R}$ par $f(x)\ =\ x^2$.
Appliquer la dérivabilité à f(x) = $x^{2}$
Indication
Ecrire la formule du nombre dérivé pour $x^2$
Déterminer la limite de $\lim_{h\to\ 0}\frac{f(a+h)-f(a)}{h}$
  1. Déterminer si la fonction f(x) est dérivable pour a = 2.

    2. ................................................................................
    ................................................................................
    ................................................................................

    $$f'(a)\ =\ \lim_{h\to\ 0}\frac{f(a+h)-f(a)}{h} $$ pour a = 2
    $$f'(2)\ =\ \lim_{h\to\ 0}\frac{f(2+h)-f(2)}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{(2+h)^{2}\ -\ (2)^2}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{\left(4\ +\ 4h\ +\ h^2\right) \ -\ 4}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{4h\ +\ h^2}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0} 4\ +\ h \ =\ 4$$ On constate que $ \lim_{x\to\ 2}\frac{f(x)\ -\ f(2)}{x-2} \ =\ 4$ la limite existe et elle est finie. Donc la fonction $x^2$ est bien dérivable en 2.

  2. Déterminer si f'(2).

    3. ................................................................................
    ................................................................................
    ................................................................................

    On vient de déterminer que $$\lim_{h\to\ 0}\frac{f(2+h)-f(2)}{h}\ \quad \Leftrightarrow \ \lim_{h\to\ 0} 4\ +\ h \ =\ 4$$ Donc le nombre dérivé de f'(2) est 4.

Activite : 17 bis
Soit $f$ définie sur $\mathbb{R}$ par $g(x)\ =\ x^2$.
  1. Déterminer le nombre dérivé de g(x) pour a = 1.

    2. ................................................................................
    ................................................................................
    ................................................................................

    $$f'(a)\ =\ \lim_{h\to\ 0}\frac{f(a+h)-f(a)}{h} $$ pour a = 1
    $$f'(1)\ =\ \lim_{h\to\ 0}\frac{f(1+h)-f(1)}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{\frac{1}{1+h}\ -\ \frac{1}{1}}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{\frac{1\ -\ \left(1+h\right)}{1+h}}{h} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{1\ -\ 1-h}{h\left(1+h\right)} $$ $$\Leftrightarrow \ \lim_{h\to\ 0}\frac{-\ h}{h\left(1+h\right)} $$ $$\Leftrightarrow \ \lim_{h\to\ 0} \frac{-1}{1+h} \ =\ -1$$ On constate que $ \lim_{h\to\ 0}\lim_{h\to\ 0}\frac{f(1+h)-f(1)}{h} \ =\ -1$ la limite existe et elle est finie. Donc la fonction $\frac{1}{x}$ est bien dérivable en 1.
    Le nombre dérivé de g(x) pour a = 1 est noté g'(1) = -1

  2. Déterminer si la fonction f(x) est dérivable pour a = 0.

    3. ................................................................................
    ................................................................................
    ................................................................................

    $$f'(a)\ =\ \lim_{x\to\ a}\frac{f(x)-f(a)}{x-a} $$ $$\Leftrightarrow \ \lim_{x\to\ a}\frac{\frac{1}{x}\ -\ \frac{1}{a}}{x-a} $$ $$\Leftrightarrow \ \lim_{x\to\ a}\frac{\frac{a\ -\ x}{a.x}}{x-a} $$ $$\Leftrightarrow \ \lim_{x\to\ a}\frac{a\ -\ x}{x.a\left(x-a\right)} $$ $$\Leftrightarrow \ \lim_{x\to\ a}\frac{-\ 1}{x.a} $$ $$\Leftrightarrow \ \lim_{x\to\ a} \frac{-1}{a.x} \ \ =\ \frac{-1}{a^{2}} $$ On constate que $ \lim_{x\to\ a}\frac{f(x)-f(a)}{x-a} \ =\ \frac{-1}{a^{2}}$.
    Pour a=0, on obtient $\lim_{x\to\ 0} \frac{-1}{0^{2}}\ =\ +\infty$ la limite n'est pas finie. Donc la fonction $\frac{1}{x}$ n'est pas dérivable en 0.

Activite : 18
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=\frac{1}{x}$. Déterminer f'(a) puis en déduire f'(3).
Appliquer la dérivabilité à f(x) = $\frac{1}{x}$
Activite : 19
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=\sqrt{x}$. Déterminer f'(a) puis en déduire f'(3).
Activite : 20
Soient les fonctions $f$ définie sur $\mathbb{R}$. Démontrer si les fonctions sont dérivables en a puis en déduire f'(a).\\

Equation de la tangente

Interprétation graphique :
Lorsque $h$ se rapproche de $0$, le point $M$ se rapproche du point $A$.
Ainsi, la droite $(AM)$ se rapproche de la tangente $\mathcal{T}$ au point $A$
$f'(a)$ correspond au coefficient directeur de la tangente $\mathcal{T}$ au point d'abscisse $a$.
Soit $f$ une fonction numérique définie sur un intervalle $I$ et dérivable en $a\in I$.
La tangente $\mathcal{T}_a$ en $a$ à la courbe $C_f$ a pour équation : $$\mathcal{T}_a\ :\ y=f'(a)(x-a)+f(a).$$
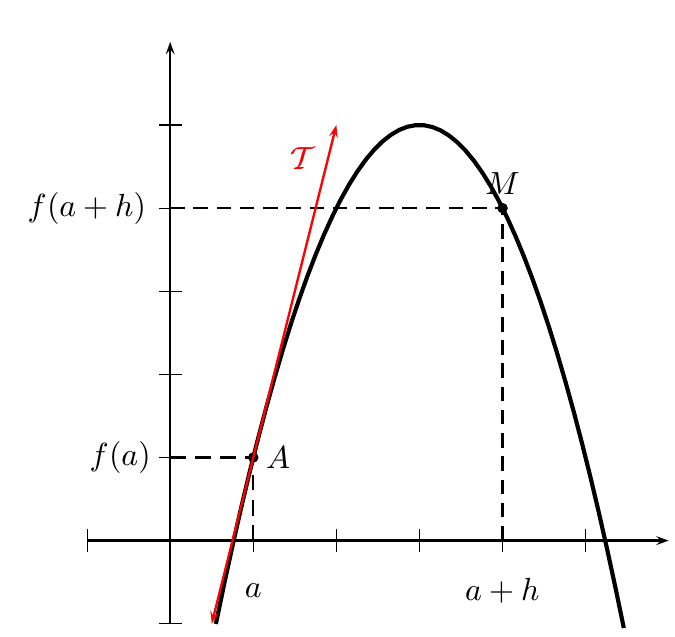
Démonstration de la tangente
Activite : 21
Soit $f(x)\ =\ x^2+2$. Déterminer les équations des tangentes en $0$ et en $-1$.
Activite : 22
Soit $f(x)\ =\ \frac{1}{x + 2}$.